技能提升

半监督学习与概率图模型

Posted by Jinming Qiao on July 28, 2020

半监督学习与概率图模型

书名：《机器学习与深度学习》

作者：周志华

概率图模型

  • 根据一些已观察到的证据来推断未知，基于概率的模型将学习任务归结为计算变量的概率分布，生成式模型先对联合分布进行建模，从而再来求解后验概率，例如：贝叶斯分类器先对联合分布进行最大似然估计，从而便可以计算类条件概率；判别式模型则是直接对条件分布进行建模

  • 概率图模型（probabilistic graphical model）是一类用图结构来表达各属性之间相关关系的概率模型，一般而言：图中的一个结点表示一个或一组随机变量，结点之间的边则表示变量间的相关关系，从而形成了一张“变量关系图”。若使用有向的边来表达变量之间的依赖关系，这样的有向关系图称为贝叶斯网（Bayesian nerwork）或有向图模型；若使用无向边，则称为马尔可夫网（Markov network）或无向图模型。

隐马尔可夫模型(HMM)
  • 隐马尔可夫模型（Hidden Markov Model，简称HMM）是结构最简单的一种贝叶斯网，在语音识别与自然语言处理领域上有着广泛的应用。HMM中的变量分为两组：状态变量与观测变量，其中状态变量一般是未知的，因此又称为“隐变量”，观测变量则是已知的输出值。在隐马尔可夫模型中，变量之间的依赖关系遵循如下两个规则：
    1. 观测变量的取值仅依赖于状态变量
    2. 下一个状态的取值仅依赖于当前状态，现在决定未来，未来与过去无关

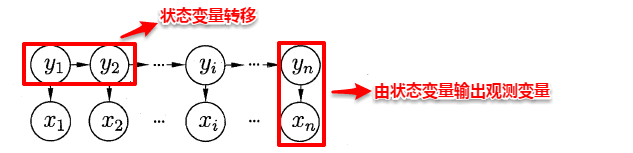
iwYPmR.png

  • 基于上述变量之间的依赖关系，我们很容易写出隐马尔可夫模型中所有变量的联合概率分布：

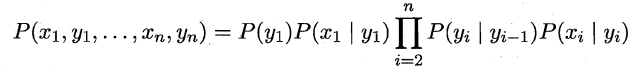
iwY9X9.png

  • 确定一个HMM模型需要以下三组参数：

iwYi01.png

  • 当确定了一个HMM模型的三个参数后，便按照下面的规则来生成观测值序列：

iwYFTx.png

  • 在实际应用中，HMM模型的发力点主要体现在下述三个问题上：

iwYEtK.png

HMM评估问题
  • HMM评估问题指的是：给定了模型的三个参数与观测值序列，求该观测值序列出现的概率。例如：对于赌场问题，便可以依据骰子掷出的结果序列来计算该结果序列出现的可能性，若小概率的事件发生了则可认为赌场的骰子有作弊的可能。解决该问题使用的是前向算法，即步步为营，自底向上的方式逐步增加序列的长度，直到获得目标概率值。在前向算法中，定义了一个前向变量，即给定观察值序列且t时刻的状态为Si的概率：

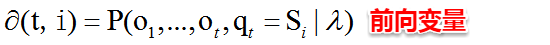
iwYVfO.png

  • 基于前向变量，很容易得到该问题的递推关系及终止条件：

iwYAk6.png

  • 因此可使用动态规划法，从最小的子问题开始，通过填表格的形式一步一步计算出目标结果。
HMM解码问题
  • HMM解码问题指的是：给定了模型的三个参数与观测值序列，求可能性最大的状态序列。例如：在语音识别问题中，人说话形成的数字信号对应着观测值序列，对应的具体文字则是状态序列，从数字信号转化为文字正是对应着根据观测值序列推断最有可能的状态值序列。解决该问题使用的是Viterbi算法，与前向算法十分类似地，Viterbi算法定义了一个Viterbi变量，也是采用动态规划的方法，自底向上逐步求解。

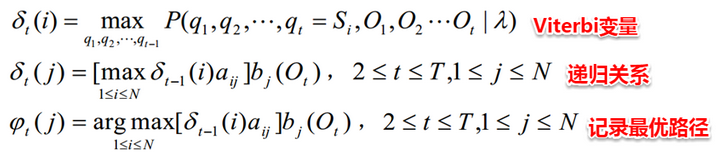
iwYepD.png

HMM学习问题
  • HMM学习问题指的是：给定观测值序列，如何调整模型的参数使得该序列出现的概率最大。这便转化成了机器学习问题，即从给定的观测值序列中学习出一个HMM模型，该问题正是EM算法的经典案例之一。其思想也十分简单：对于给定的观测值序列，如果我们能够按照该序列潜在的规律来调整模型的三个参数，则可以使得该序列出现的可能性最大。假设状态值序列也已知，则很容易计算出与该序列最契合的模型参数：

iwYm1e.png

  • 但一般状态值序列都是不可观测的，且即使给定观测值序列与模型参数，状态序列仍然遭遇组合爆炸。因此上面这种简单的统计方法就行不通了，若将状态值序列看作为隐变量，这时便可以考虑使用EM算法来对该问题进行求解：
    1. 首先对HMM模型的三个参数进行随机初始化；
    2. 根据模型的参数与观测值序列，计算t时刻状态为i且t+1时刻状态为j的概率以及t时刻状态为i的概率。

iwYn6H.png

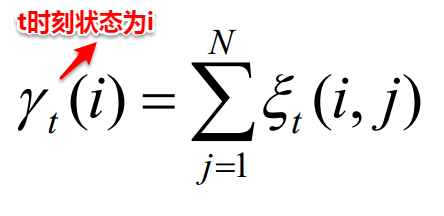
iwYdns.png

  • 接着便可以对模型的三个参数进行重新估计：

iwYY9S.png

  • 重复步骤2-3，直至三个参数值收敛，便得到了最终的HMM模型。
马尔可夫随机场（MRF）
  • 马尔可夫随机场（Markov Random Field）是一种典型的马尔可夫网，即使用无向边来表达变量间的依赖关系。在马尔可夫随机场中，对于关系图中的一个子集，若任意两结点间都有边连接，则称该子集为一个团；若再加一个结点便不能形成团，则称该子集为极大团。MRF使用势函数来定义多个变量的概率分布函数，其中每个（极大）团对应一个势函数，一般团中的变量关系也体现在它所对应的极大团中，因此常常基于极大团来定义变量的联合概率分布函数。具体而言，若所有变量构成的极大团的集合为C，则MRF的联合概率函数可以定义为：

iwYGh8.png

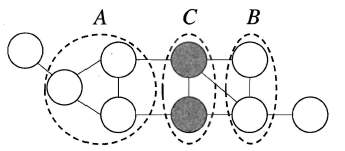
  • 对于条件独立性，马尔可夫随机场通过分离集来实现条件独立，若A结点集必须经过C结点集才能到达B结点集，则称C为分离集。书上给出了一个简单情形下的条件独立证明过程，十分贴切易懂，此处不再展开。基于分离集的概念，得到了MRF的三个性质：
    1. 全局马尔可夫性：给定两个变量子集的分离集，则这两个变量子集条件独立。
    2. 局部马尔可夫性：给定某变量的邻接变量，则该变量与其它变量条件独立。
    3. 成对马尔可夫性：给定所有其他变量，两个非邻接变量条件独立。

iwY07q.png

  • 对于MRF中的势函数，势函数主要用于描述团中变量之间的相关关系，且要求为非负函数，直观来看：势函数需要在偏好的变量取值上函数值较大，例如：若x1与x2成正相关，则需要将这种关系反映在势函数的函数值中。一般我们常使用指数函数来定义势函数：

iwY8tf.png

条件随机场（CRF）
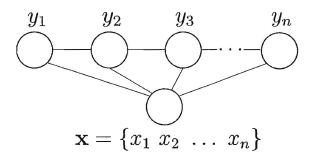
  • 隐马尔可夫模型和马尔可夫随机场都属于生成式模型，即对联合概率进行建模，条件随机场则是对条件分布进行建模。CRF试图在给定观测值序列后，对状态序列的概率分布进行建模，即P(y x)。直观上看：CRF与HMM的解码问题十分类似，都是在给定观测值序列后，研究状态序列可能的取值。CRF可以有多种结构，只需保证状态序列满足马尔可夫性即可，一般我们常使用的是链式条件随机场：

iwYt1g.png

  • 与马尔可夫随机场定义联合概率类似地，CRF也通过团以及势函数的概念来定义条件概率P(y x)。在给定观测值序列的条件下，链式条件随机场主要包含两种团结构：单个状态团及相邻状态团，通过引入两类特征函数便可以定义出目标条件概率：

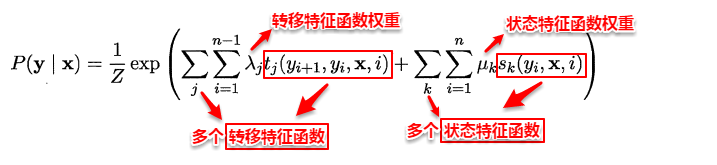
iwYNcQ.png

  • 转移特征函数主要判定两个相邻的标注是否合理，例如：动词+动词显然语法不通；状态特征函数则判定观测值与对应的标注是否合理，例如： ly结尾的词–>副词较合理。因此我们可以定义一个特征函数集合，用这个特征函数集合来为一个标注序列打分，并据此选出最靠谱的标注序列。也就是说，每一个特征函数（对应一种规则）都可以用来为一个标注序列评分，把集合中所有特征函数对同一个标注序列的评分综合起来，就是这个标注序列最终的评分值。可以看出：特征函数是一些经验的特性。
学习与推断
  • 对于生成式模型，通常我们都是先对变量的联合概率分布进行建模，接着再求出目标变量的边际分布（marginal distribution），变量消去与信念传播。
变量消去
  • 变量消去利用条件独立性来消减计算目标概率值所需的计算量，它通过运用乘法与加法的分配率，将对变量的积的求和问题转化为对部分变量交替进行求积与求和的问题，从而将每次的运算控制在局部，达到简化运算的目的。

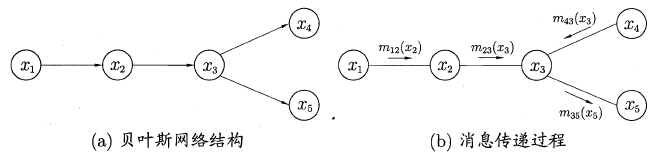
iwYUXj.png

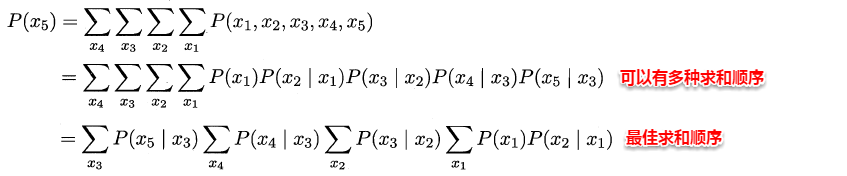
iwYwBn.png

信念传播
  • 若将变量求和操作看作是一种消息的传递过程，信念传播可以理解成：一个节点在接收到所有其它节点的消息后才向另一个节点发送消息，同时当前节点的边际概率正比于他所接收的消息的乘积：

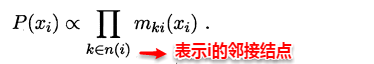
iwYDA0.png

  • 因此只需要经过下面两个步骤，便可以完成所有的消息传递过程。利用动态规划法的思想记录传递过程中的所有消息，当计算某个结点的边际概率分布时，只需直接取出传到该结点的消息即可，从而避免了计算多个边际分布时的冗余计算问题。
    1. 指定一个根节点，从所有的叶节点开始向根节点传递消息，直到根节点收到所有邻接结点的消息（从叶到根）；
    2. 从根节点开始向叶节点传递消息，直到所有叶节点均收到消息（从根到叶）。

iwYgc4.png

FEATURED TAGS
项目开发 知识总结 论文解读 技能提升 好书共享 学习思考
FRIENDS